3. 단순 선형 회귀

3. 단순 선형 회귀

선형 회귀란 종속변수 y와 한 개 이상의 독립변수 X와의 선형 상관 관계를 모델링하는 것.

이 때, 독립변수 X가 한 개라면, 단순 선형 회귀라고 한다.

그렇다면,

독립변수 x에 대해 종속변수 y값을 표현하는 모델을 만든다는 것.

쉽게 표현하면, x값이 있을 때 y는 얼마인가? (단, y는 x에 영향을 받는 값이다.)

몸무게에 대하여 키를 예측하는 선형 회귀 모델.

파란점이 실제 data, 빨간 선이 모델이 예측한 값이다.

잠깐만요, 이 예측이 더 좋은 예측아닌가요?

img

이게 훨씬 더 데이터를 잘 표현하는데, 이게 더 잘 학습된 모델이 아닌가요?

정답을 말해주자면, 틀렸다.

이건 학습이 잘못된 모델이다!

어째서 학습이 잘못됐다고 하는가?

이전 강에서 봤듯,

우리는 모델이 추측을 잘 하기를 기대한다. 그래서 학습을 한다.

위 모델은 기존 데이터는 잘 추측하겠지만, 새로운 데이터를 주면 추측에 실패할 확률이 높다.

위의 키와 몸무게 분석을 예시로 들어보자면,

키가 큰데, 몸무게가 매우 가벼운 사람이 있을 수 있고, 키가 작은데, 몸무게가 매우 무거운 사람이 있을 수 있다.

이런 특이 데이터가 일부 존재할 수 있다!

그래서 처음 보는 데이터도 얼추 맞추기를 원한다면,

특이 데이터가 있을 수 있으니 기존에 알고있는 data에 너무 fitting(학습)하지 말고 적당히 해야한다!

img

이게 잘 fitting(학습)된 모델이다.

현재 data에 대해서 살짝 오차가 있지만,

처음보는 데이터여도 얼추 맞출 수 있을 것이다!

img

너무 적게 학습한 것도 당연히 나쁩니다.

우리의 목표는, 대부분의 경우에 적은 오차를 가치는 모델을 만드는 것.

이름이 왜 선형회귀인가?

여기서의 회귀란, 평균으로의 회귀를 의미한다.

이는 아래와 같이 이해할 수 있다.

img

이는 정규분포 곡선이다.

대부분 평균에 몰려있고, 평균에서 멀어질수록 확률은 급감한다.

그래서 적절한 추측을 하기 위해서, 평균으로의 회귀를 하여 추측하겠다는 뜻.

그러면, 특이값이 존재하더라도 영향을 덜 받을 것이다.

이는 오차가 줄어든다는 뜻이며, 우리가 바라는 것이다!

선형이란, 파라미터의 관계가 선형이라는 것!

Quiz 1.

X = [1, 2, 3]일 때,

Y = [3, 5, 7]이다.

X = 4일 때, Y의 값은 얼마인가?

정답은 9이다.

Quiz 2.

왜 9인가?

어떻게 y = 2x + 1의 관계를 알아냈는가?

무의식 중에, * 2를 해봤을 것이다.

그랬을 때, 1 차이가 난다는 사실을 인지 했을 것이고,

최종적으로 y = 2x + 1이라고 판단을 내렸을 것이다.

이를 다시 해석하면,

1. 초기값 x를 설정하여 테스트 한다.

2. 정답에 가까워 지는 방향으로 x를 수정.

3. 수정된 x를 이용하여 다시 테스트.

4. 정답에 맞을 때 까지 2 ~ 3번 과정을 반복한다.

모델도 똑같은 과정을 거쳐 학습을 한다!

선형회귀 학습 과정

$$X = [1, 2, 3]$$

$$Y = [3, 5, 7]$$

가설 함수 (Hypothesis function)

우리의 예측은, 직선 형태이다. 즉 기울기와 절편 두가지 값이 필요하다.

$$H(W,b) = Wx + b$$

우리의 목표는 W=2, b=1 이다.

1번 과정, 가설 초기화

먼저, 1번 과정이다, 일단 아무거나 넣고 테스트 한다.

초기 값,

$$W=1, b=0$$

$$y = x$$

가 된다.

img

이제 2번과정이다, 정답에 가까워 지는 방향으로 W와 b를 수정할 차례.

잠깐, 정답에 가까워지는 방향이란 무엇인가?

예측값과 실제값의 차이, 오차.

즉, 오차가 줄어드는 방향으로 W와 b를 수정해야한다.

오차 계산 함수(Cost function)

$$Cost(W, b) = {1 \over m} \times \Sigma_{i=1}^{m}(W_{x_{i}}+b-y_{i})^{2}$$

$$W_{x_{i}}+b$$

는 우리의 예측값이다!

보기 편하게 하기 위해서, 예측값을 $\hat{y_{i}}$ 이라 표기한다.

$$Cost(W, b) = {1 \over m} \times \Sigma_{i=1}^{m}(\hat{y_{i}}-y_{i})^{2}$$

오차 제곱의 평균. 이 수치를 0에 가깝게 줄여야 한다!

외 제곱 오차를 사용하는지는 수업 마지막에 추가설명이 있습니다.

W에 대한 오차 그래프

img

W가 2일 때가 정답이므로, 2에서 오차값이 젤 작아야 한다.

또한 2에서 멀어질 수록 오차가 커지기 때문에 볼록 함수 형태가 된다.

즉, 기울기가 0이 되는 지점이 최소 오차값.

img

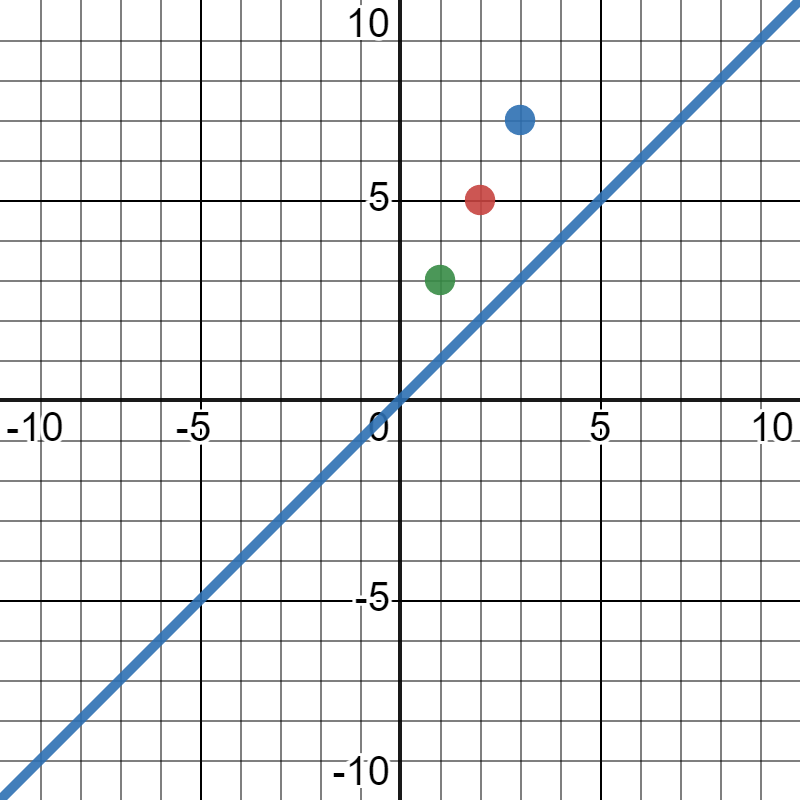
초기값이 녹색점 또는 파란점이라 하자.

어느 쪽으로 이동해야 최소 오차가 되는가?

기울기가 0인 지점으로 이동해야 최소 오차가 된다.

2번 과정. 기울기가 0인 지점을 찾는 법. 경사하강법(Gradient descent)

img

기울기가 0인 지점보다 값이 작으면, 기울기가 음수일 것이다.

기울기가 0인 지점보다 값이 작으면, 양의 방향으로 갱신해야 한다.

기울기가 0인 지점보다 값이 크면, 기울기가 양수일 것이다.

기울기가 0인 지점보다 값이 크면, 음의 방향으로 갱신해야 한다.

즉, 기울기의 반대 방향으로 값을 갱신하면, 무조건 오차가 줄어든다.

이를 경사 하강법(Gradient descent)라고 한다.

다시 흐름을 정리 해 보자.

1번 과정. 초기값 설정,

2번 과정. 테스트 후 X값 갱신.

3번 과정. 다시 테스트

4번 과정. 충족할때까지 2 ~ 3번 과정의 반복.

경사 하강법을 이용하여 X값 갱신을 시킬 수 있게 되었다.

3번 과정. 테스트와 업데이트의 반복

우린 W와 b이 두가지를 업데이트 해야한다.

그럼 W에 대한 Cost-function과 b에 대한 Cost-function을 따로따로 구하고,

각각 경사하강법을 적용하여 W와 b를 최적화 해야한다.

X축을 W로 한 Cost-function와, X축을 b로한 Cost-function이 필요하다. 이를 각 W-그래프, b-그래프라 임시로 칭한다.

기울기의 반대 방향으로 가면 된다고 했는데, 기울기는 미분이다.

W-그래프에서 기울기에 영향을 주는 X축이 W인데 수식은 $W_{x_{i}}+b$ 이다.

b-그래프에서 기울기에 영향을 주는 X축이 b인데 수식은 $W_{x_{i}}+b$ 이다.

그래서 편미분을 이용하여 기울기를 구한다.

$$W의 기울기 = {\partial\ Cost(W, b) \over \partial\ W}$$

$$b의 기울기 = {\partial\ Cost(W, b) \over \partial\ b}$$

즉, 경사하강법을 이용한 W, b값의 조정은 아래와 같다. a는, 갱신되는 크기를 조절하기 위한 상수이다. (learning-rate)

$$W = W - \alpha{\partial\ Cost(W, b) \over \partial\ W}$$

$$b = b - \alpha{\partial\ Cost(W, b) \over \partial\ b}$$

위의 수식을 반복하여, 오차가 최적화 될 떄까지 반복하고,

결국에 W와 b값을 얻게되어, 선형 회귀 모델이 완성된다.

부록

잠깐, 왜 오차의 평균이 아니라 오차 제곱의 평균인가요?

오차에 부호가 있으면 안되기 떄문입니다!

img

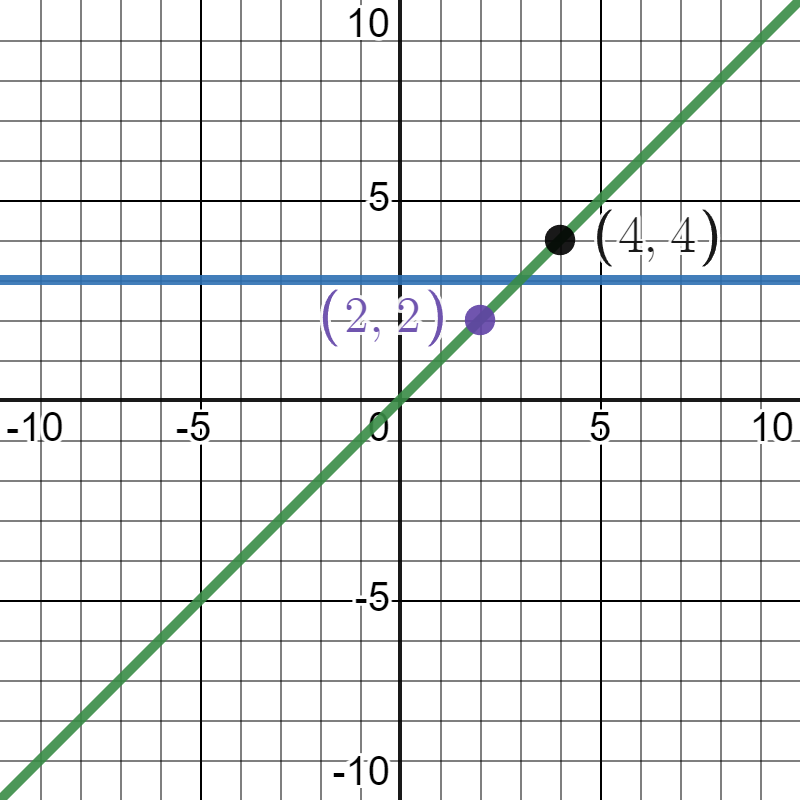
초록색 선이 우리가 기대하는 모델의 예측이다.

파란색 선도 오차가 0이다. +1 오차와 -1 오차가 있어 오차의 합이 0이 된다..

부호는 없애야 한다!

부호를 없애는 방법, (절댓값 Vs 제곱)

MAE(Mean Absolute Error)

절대 오차의 평균.

img

절댓값을 사용하여 Cost-function을 계산하면, 고정적인 크기 만큼 이동하게 된다.

한 번에 많이 움직이면, 기울기가 0인 최소 오차지점을 넘어갈 수도 있다.

MSE(Mean Suquared Error)

제곱 오차의 평균

img

절댓값과 제곱 둘 다 부호를 없앤다는 공통점이 있다.

그럼 차이점은, 제곱을하냐 안하냐 차이이다.

제곱은 값을 극대화 시키는 특성이 있다.

$${0.1}^{2}=0.01$$

$${10}^{2}=100$$

위의 수식에서 볼 수 있듯이,

작은 값을 더욱 작게하고, 큰 값을 더욱 크게하는 극대화 특성을 가진다.

즉, 기울기가 0인지점(최소 오차지점)에 갈수록 조금씩 갱신을 하게 된다는 것이며,

이는 기울기가 0인지점(최소 오차지점)을 지나칠 가능성을 줄인다.

그래서 주로 MSE를 사용하지만, MAE가 더 좋을 때도 있다는 점!

Python으로 복습하는 단순 선형 회귀

!pip install numpy

Collecting numpy
  Using cached numpy-1.24.2-cp311-cp311-win_amd64.whl (14.8 MB)
Installing collected packages: numpy
Successfully installed numpy-1.24.2



[notice] A new release of pip available: 22.3.1 -> 23.0.1
[notice] To update, run: python.exe -m pip install --upgrade pip

import numpy as np

x_train = np.array([1., 2., 3., 4., 5., 6.])
y_train = np.array([9., 16., 23., 30., 37., 44.])

W = 0.0
b = 0.0

n_data = len(x_train)

epochs = 5000
learning_rate = 0.01

for i in range(epochs):
    hypothesis = x_train * W + b
    cost = np.sum((hypothesis - y_train) ** 2) / n_data
    gradient_w = np.sum((W * x_train - y_train + b) * 2 * x_train) / n_data
    gradient_b = np.sum((W * x_train - y_train + b) * 2) / n_data

    W -= learning_rate * gradient_w
    b -= learning_rate * gradient_b

    if i % 100 == 0:
        print('Epoch ({:10d}/{:10d}) cost: {:10f}, W: {:10f}, b:{:10f}'.format(i, epochs, cost, W, b))

print('W: {:10f}'.format(W))
print('b: {:10f}'.format(b))
print('result : ')
print(x_train * W + b)

Epoch (         0/      5000) cost: 845.166667, W:   2.263333, b:  0.530000
Epoch (       100/      5000) cost:   0.011092, W:   7.055875, b:  1.760787
Epoch (       200/      5000) cost:   0.005339, W:   7.038765, b:  1.834041
Epoch (       300/      5000) cost:   0.002570, W:   7.026894, b:  1.884862
Epoch (       400/      5000) cost:   0.001237, W:   7.018658, b:  1.920121
Epoch (       500/      5000) cost:   0.000595, W:   7.012945, b:  1.944582
Epoch (       600/      5000) cost:   0.000287, W:   7.008981, b:  1.961552
Epoch (       700/      5000) cost:   0.000138, W:   7.006230, b:  1.973326
Epoch (       800/      5000) cost:   0.000066, W:   7.004323, b:  1.981494
Epoch (       900/      5000) cost:   0.000032, W:   7.002999, b:  1.987161
Epoch (      1000/      5000) cost:   0.000015, W:   7.002081, b:  1.991093
Epoch (      1100/      5000) cost:   0.000007, W:   7.001443, b:  1.993820
Epoch (      1200/      5000) cost:   0.000004, W:   7.001001, b:  1.995713
Epoch (      1300/      5000) cost:   0.000002, W:   7.000695, b:  1.997026
Epoch (      1400/      5000) cost:   0.000001, W:   7.000482, b:  1.997936
Epoch (      1500/      5000) cost:   0.000000, W:   7.000334, b:  1.998568
Epoch (      1600/      5000) cost:   0.000000, W:   7.000232, b:  1.999007
Epoch (      1700/      5000) cost:   0.000000, W:   7.000161, b:  1.999311
Epoch (      1800/      5000) cost:   0.000000, W:   7.000112, b:  1.999522
Epoch (      1900/      5000) cost:   0.000000, W:   7.000077, b:  1.999668
Epoch (      2000/      5000) cost:   0.000000, W:   7.000054, b:  1.999770
Epoch (      2100/      5000) cost:   0.000000, W:   7.000037, b:  1.999840
Epoch (      2200/      5000) cost:   0.000000, W:   7.000026, b:  1.999889
Epoch (      2300/      5000) cost:   0.000000, W:   7.000018, b:  1.999923
Epoch (      2400/      5000) cost:   0.000000, W:   7.000012, b:  1.999947
Epoch (      2500/      5000) cost:   0.000000, W:   7.000009, b:  1.999963
Epoch (      2600/      5000) cost:   0.000000, W:   7.000006, b:  1.999974
Epoch (      2700/      5000) cost:   0.000000, W:   7.000004, b:  1.999982
Epoch (      2800/      5000) cost:   0.000000, W:   7.000003, b:  1.999988
Epoch (      2900/      5000) cost:   0.000000, W:   7.000002, b:  1.999991
Epoch (      3000/      5000) cost:   0.000000, W:   7.000001, b:  1.999994
Epoch (      3100/      5000) cost:   0.000000, W:   7.000001, b:  1.999996
Epoch (      3200/      5000) cost:   0.000000, W:   7.000001, b:  1.999997
Epoch (      3300/      5000) cost:   0.000000, W:   7.000000, b:  1.999998
Epoch (      3400/      5000) cost:   0.000000, W:   7.000000, b:  1.999999
Epoch (      3500/      5000) cost:   0.000000, W:   7.000000, b:  1.999999
Epoch (      3600/      5000) cost:   0.000000, W:   7.000000, b:  1.999999
Epoch (      3700/      5000) cost:   0.000000, W:   7.000000, b:  2.000000
Epoch (      3800/      5000) cost:   0.000000, W:   7.000000, b:  2.000000
Epoch (      3900/      5000) cost:   0.000000, W:   7.000000, b:  2.000000
Epoch (      4000/      5000) cost:   0.000000, W:   7.000000, b:  2.000000
Epoch (      4100/      5000) cost:   0.000000, W:   7.000000, b:  2.000000
Epoch (      4200/      5000) cost:   0.000000, W:   7.000000, b:  2.000000
Epoch (      4300/      5000) cost:   0.000000, W:   7.000000, b:  2.000000
Epoch (      4400/      5000) cost:   0.000000, W:   7.000000, b:  2.000000
Epoch (      4500/      5000) cost:   0.000000, W:   7.000000, b:  2.000000
Epoch (      4600/      5000) cost:   0.000000, W:   7.000000, b:  2.000000
Epoch (      4700/      5000) cost:   0.000000, W:   7.000000, b:  2.000000
Epoch (      4800/      5000) cost:   0.000000, W:   7.000000, b:  2.000000
Epoch (      4900/      5000) cost:   0.000000, W:   7.000000, b:  2.000000
W:   7.000000
b:   2.000000
result : 
[ 9. 16. 23. 30. 37. 44.]